ニュートン法の更新式を導出
ニュートン法の更新式を導出してみる。
導出
最小化したい損失関数を$L(\boldsymbol{w})$とする。
$k$ステップ目において、$L(\boldsymbol{w})$を$\boldsymbol{w}=\boldsymbol{w}_{k}$においてテイラー展開によって2次近似すると、
\[L(\boldsymbol{w}) \approx L(\boldsymbol{w}_{k}) + \Delta \boldsymbol{w}^{T} \nabla L(\boldsymbol{w}_{k}) + \cfrac{1}{2}\Delta\boldsymbol{w}^{T} \left(\nabla^{2} L(\boldsymbol{w}_{k})\right) \Delta\boldsymbol{w} \quad (\Delta\boldsymbol{w}=\boldsymbol{w}-\boldsymbol{w}_{k})\]ここで、$\nabla L(\boldsymbol{w}_{k})$は勾配ベクトル、$\nabla^{2} L(\boldsymbol{w}_{k})$はヘッセ行列である。
\[\begin{equation} \nabla L(\boldsymbol{x}) = \begin{bmatrix} \cfrac{\partial L(\boldsymbol{x})}{\partial x_{1}} \\ \cfrac{\partial L(\boldsymbol{x})}{\partial x_{2}} \\ \vdots \\ \cfrac{\partial L(\boldsymbol{x})}{\partial x_{n}} \end{bmatrix} \end{equation}\] \[\begin{equation} \nabla^{2} L(\boldsymbol{x}) = \begin{bmatrix} \cfrac{\partial^{2} L(\boldsymbol{x})}{\partial x_{1}^{2}} & \cfrac{\partial^{2} L(\boldsymbol{x})}{\partial x_{1}x_{2}} & \cdots & \cfrac{\partial^{2} L(\boldsymbol{x})}{\partial x_{1}x_{n}} \\ \cfrac{\partial^{2} L(\boldsymbol{x})}{\partial x_{2}x_{1}} & \cfrac{\partial^{2} L(\boldsymbol{x})}{\partial x_{2}^{2}} & \cdots & \cfrac{\partial^{2} L(\boldsymbol{x})}{\partial x_{2}x_{n}} \\ \vdots & \vdots & & \vdots \\ \cfrac{\partial^{2} L(\boldsymbol{x})}{\partial x_{n}x_{1}} & \cfrac{\partial^{2} L(\boldsymbol{x})}{\partial x_{n}x_{2}} & \cdots & \cfrac{\partial^{2} L(\boldsymbol{x})}{\partial x_{n}^{2}} \end{bmatrix} \end{equation}\]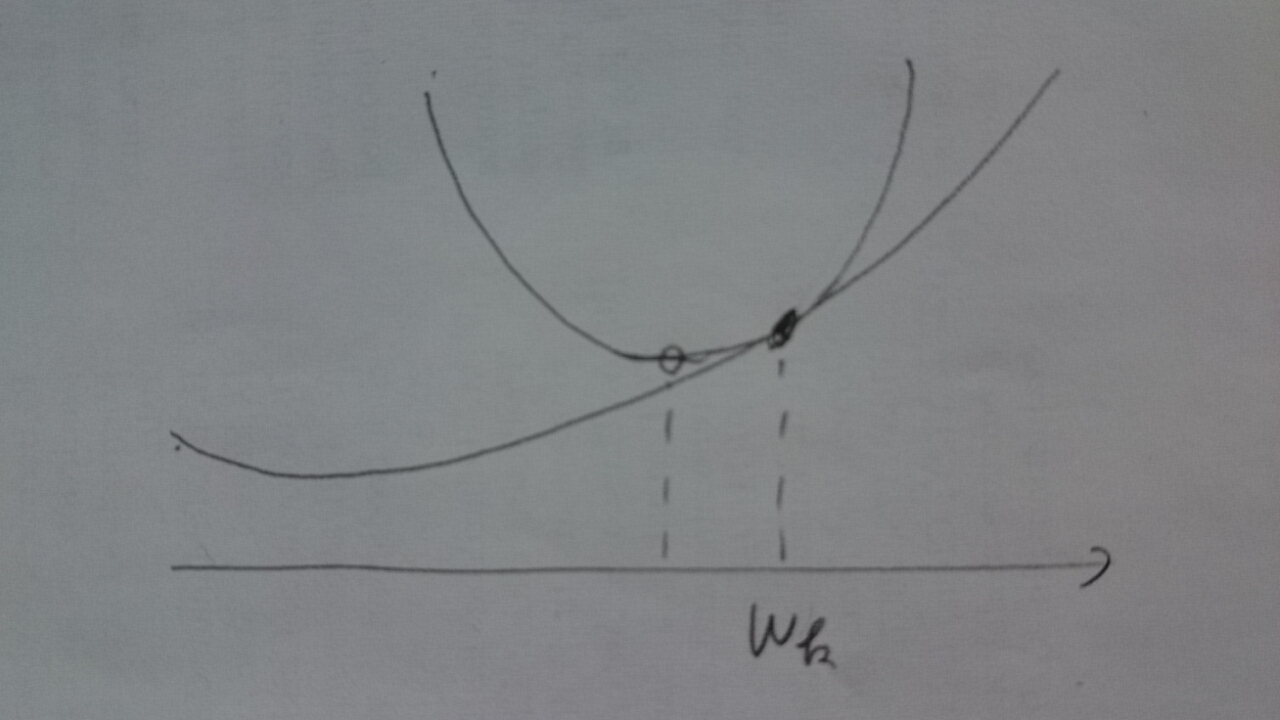
右辺を$\Delta\boldsymbol{w}$の関数$h(\Delta{\boldsymbol{w}})$と見ると
$h(\Delta{\boldsymbol{w}})$は$\Delta\boldsymbol{w}$の2次関数になり、
ヘッセ行列$\nabla^{2} L(\boldsymbol{w_{k}})$が正定値対称行列であれば
$h(\Delta{\boldsymbol{w}})$は唯一の最小値をとる。
$\boldsymbol{g}_{k}=\nabla L(\boldsymbol{w}_{k})$、 $\boldsymbol{H}_{k}=\nabla^{2} L(\boldsymbol{w_{k}})$とおき、 $h(\Delta{\boldsymbol{w}})$を$\Delta{\boldsymbol{w}}$で微分すると、
\[\cfrac{\partial h(\Delta{\boldsymbol{w}})}{\partial \Delta{\boldsymbol{w}}} = \boldsymbol{g}_{k} + \boldsymbol{H}_{k}\Delta \boldsymbol{w}\]この式が0になる(=$h(\Delta{\boldsymbol{w}})$が最小値をとる)とき、
\[\Delta\boldsymbol{w}=-\boldsymbol{H}_{k}^{-1}\boldsymbol{g}_{k}\]となる。
$\Delta\boldsymbol{w}=\boldsymbol{w}-\boldsymbol{w}_{k}$なので、
\[\boldsymbol{w} = \boldsymbol{w}_{k} + \Delta\boldsymbol{w}\]ステップ幅を$\alpha_{k}$とすると、
\[\boldsymbol{w}_{k+1} = \boldsymbol{w}_{k} - \alpha_{k}\boldsymbol{H}_{k}^{-1}\boldsymbol{g}_{k}\]として更新される。
特徴
- 2次収束する
- ヘッセ行列が正定値対称行列となるときのみ収束性が保証される
- ヘッセ行列の逆行列を計算する必要があるが、計算量は$O(n^{3})$なので陽に求めづらい。
- そこで逆行列を近似的に求める準ニュートン法(quasi-Newton method)に発展する。