みどりぼん 第7章 一般化線形混合モデル
みどりぼん第7章のGLMMについてまとめた。
使用したデータはこちら。 また、jupyter notebookはこちら。
GLMで説明できないデータ
100個体の架空植物から取り出した8個の種子のうちいくつが生存しているかに対して、
葉数の増加がどう影響しているのかを調べる。
>>> import numpy as np
>>> import pandas as pd
>>> import matplotlib.pyplot as plt
>>> import matplotlib.cm as cm
>>> import matplotlib.font_manager as fm
>>>
>>> data = pd.read_csv('~/Downloads/data.csv')
>>> fp = fm.FontProperties(fname='/Library/Fonts/Yu Gothic Medium.otf', size=12)
>>> data.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 100 entries, 0 to 99
Data columns (total 4 columns):
N 100 non-null int64
y 100 non-null int64
x 100 non-null int64
id 100 non-null int64
dtypes: int64(4)
memory usage: 3.2 KB
>>> data.describe()
N y x id
count 100.0 100.000000 100.000000 100.000000
mean 8.0 3.810000 4.000000 50.500000
std 0.0 3.070534 1.421338 29.011492
min 8.0 0.000000 2.000000 1.000000
25% 8.0 1.000000 3.000000 25.750000
50% 8.0 3.000000 4.000000 50.500000
75% 8.0 7.000000 5.000000 75.250000
max 8.0 8.000000 6.000000 100.000000
個体数は100個であり、
- $N$: 1個体から取り出す種子数 (8個で固定)
- $y$: 生存種子数
- $x$: 葉数
- id: 個体に振られた番号
である。
>>> data_for_plot = data.groupby(['x', 'y']).size().reset_index().rename(columns={0: 'num'})
>>> fig = plt.figure()
>>> ax = fig.add_subplot(1, 1, 1)
>>> # http://matplotlib.org/examples/color/colormaps_reference.html
>>> fig.colorbar(ax.scatter(data_for_plot.x, data_for_plot.y, c=data_for_plot.num, cmap=cm.Blues))
>>> ax.set_xlabel('葉数 x', fontproperties=fp)
>>> ax.set_ylabel('生存種子数 y', fontproperties=fp)
>>> ax.set_title('全100個体のxとy', fontproperties=fp)
>>> fig.show()
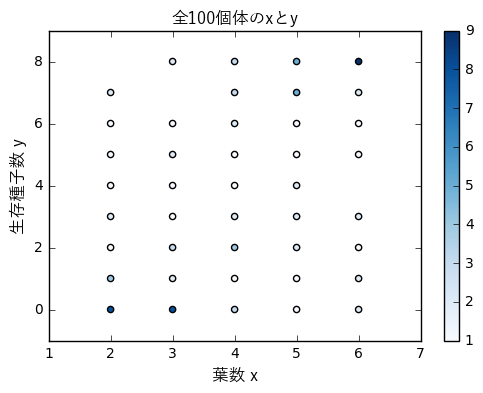
葉数と生存種子数の関係を示す散布図である。
色が濃いほど多くの点が重なっていることを示す。
例えば、$x=6$で$y=8$の個体数は9である。
ロジスティック回帰でfitting
「$N$個の種子のうち$y$個が生存した」というカウントデータなので
ロジスティック回帰でモデリングする。
個体$i$での種子の生存確率$q_{i}$が葉数$x_{i}$に依存するので
線形予測子とロジットリンク関数を組み合わせて以下の式で表される。
>>> import statsmodels.api as sm
>>> import statsmodels.formula.api as smf
>>> glm = smf.glm(formula='y + I(N - y) ~ x', data=data,
... family=sm.families.Binomial())
>>> res = glm.fit()
>>> res.summary()
<class 'statsmodels.iolib.summary.Summary'>
"""
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: ['y', 'I(N - y)'] No. Observations: 100
Model: GLM Df Residuals: 98
Model Family: Binomial Df Model: 1
Link Function: logit Scale: 1.0
Method: IRLS Log-Likelihood: -322.80
Date: Tue, 20 Dec 2016 Deviance: 513.84
Time: 17:14:46 Pearson chi2: 428.
No. Iterations: 6
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept -2.1487 0.237 -9.057 0.000 -2.614 -1.684
x 0.5104 0.056 9.179 0.000 0.401 0.619
==============================================================================
"""
>>> N = 8
>>> xrange = np.arange(min(data.x), max(data.x), (max(data.x) - min(data.x)) / 100)
>>> x_test = pd.DataFrame({'x': xrange})
>>> y_test = res.predict(x_test)
>>>
>>> fig.show()
>>> fig = plt.figure()
>>> ax = fig.add_subplot(1, 1, 1)
>>> fig.colorbar(ax.scatter(data_for_plot.x, data_for_plot.y, c=data_for_plot.num, cmap=cm.Blues))
>>> ax.plot(x_test, y_test * N, label='C')
>>> ax.set_xlabel('葉数 x', fontproperties=fp)
>>> ax.set_ylabel('生存種子数 y', fontproperties=fp)
>>> ax.set_title('葉数と生存種子数の関係', fontproperties=fp)
>>> fig.show()
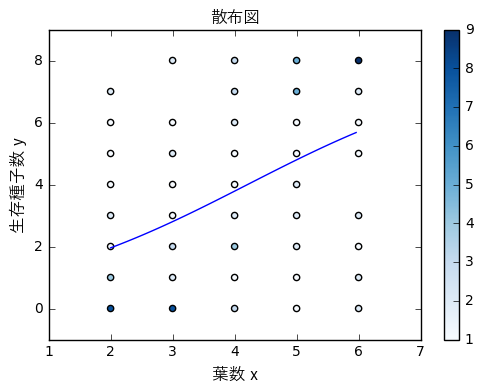
$x=4$のときの生存種子数ごとの個体数と推定したモデルから二項分布で求めた個体数だが、
まるで一致していない。
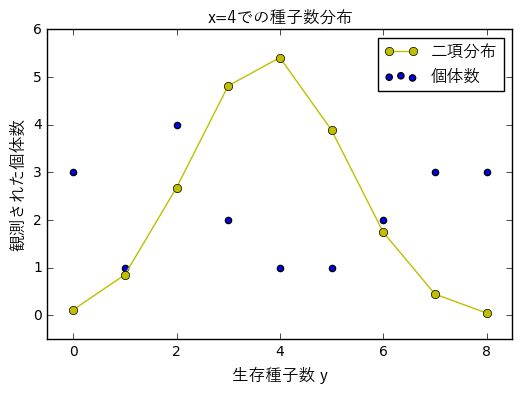
過分散と個体差
このデータはロジスティック回帰で推定したモデルよりも分散が大きい。
これを過分散と呼ぶ。
GLMでは説明変数(このデータであれば葉数)が同じであれば
目的変数の値も同じになる、つまりどの個体も均質であると仮定しているが、
実際には観測されていない個体差や場所差があり、それによって分散の大きさがもたらされている。
現実には影響を与えている全ての要因を特定・定量化することは不可能なため、
個体差を原因不明のまま、統計モデリングに取り込む必要がある。
ここで一般化線形混合モデル(GLMM)が用いられる。
一般化線形混合モデル (GLMM)
式($\ref{eq:tag1})$に個体$i$の個体差を表すパラメータ$r_{i}$を追加する。
\[logit(q_{i})=\beta_{1}+\beta_{2}x_{i}+r_{i} \tag{2}\]$r_{i}$が確率分布にしたがうと仮定するのがGLMMの特徴である。
$\beta_{1}+\beta_{2}x_{i}$を固定効果(random effects)、$r_{i}$をランダム効果(random effects)と呼ぶ。
反復・疑似反復
GLMMを採用するかどうかの判断のポイントは、
GLMによるモデリングでは過分散になるかどうかよりも、
個体差・場所差が識別できてしまうデータの取り方をしているか、
つまり疑似反復をしているかどうかである。
「個体から複数のデータをとる」ことを擬似反復といい、
同じ個体から得られたデータは似た傾向を持つと考えられるため、
個体差を考慮しなければ推定結果に偏りが生じるためである。
(A) 個体・植木鉢が反復
- 1個体/植木鉢 かつ 1種子/個体
- 個体差と植木鉢差を区別できない
- GLMで推定して問題ない
(B) 個体は疑似反復、植木鉢は反復
- 1個体/植木鉢 かつ n種子/個体
- e.x. 個体Aから得られた種子は生きてるのが多いが、
個体Bから得られた種子は死んでいるのが多い - 植木鉢に植わっている個体は1つだけなので、
その差が個体差によるものか植木鉢差によるものか区別できない - 個体差を考慮したGLMMで推定する
(C) 個体は反復・植木鉢は疑似反復
- n個体/植木鉢 かつ 1種子/個体
- e.x. 植木鉢Aから得られた種子は死んでいるのが多いが、
植木鉢Bから得られた種子は生きているのが多い - 個体から得る種子は1つだけなので、
その差が個体差によるものか植木鉢差によるものか区別できない - 植木鉢差を考慮したGLMMで推定する
(D) 個体・植木鉢が擬似反復
- n個体/植木鉢 かつ n種子/個体
- 個体差・植木鉢差を考慮したGLMMで推定する
なお、(D)のように2つのランダム効果を考慮しながら最尤推定するのは難しいので、
GLMMと最尤推定ではなくベイズモデルとMCMCが実際にはよく使われる?
まとめ
- GLMでは全個体が均質と仮定してモデリングするが、
現実のデータでは個体差が存在するため、
GLMによるモデリングよりも過分散になる - 個体差・場所差を組み込んだモデリングをおこなうには
一般化線形混合モデル(GLMM)を使用する - GLMMを適用するのはデータが過分散となるかどうかよりも
- 擬似反復となるようなデータの取り方をしているかどうかである