みどりぼん 第6章 割算値モデリングのためのオフセット項
みどりぼん第6章の割算値モデリングのためのオフセット項についてまとめた。
使用したデータはこちら。 また、jupyter notebookはこちら。
割算値モデリングのためのオフセット項
- 調査地$i$ごとにその面積$A_{i}$が異なる
- 調査地$i$における植物個体数$y_{i}$を記録
- 調査地$i$の明るさ$x_{i}$から人口密度$z_{i}$を推定する
平均個体数を$\lambda_{i}$とすると、面積$A_{i}$と人口密度$z_{i}$の関係は
\[\cfrac{\lambda_{i}}{A_{i}}=z_{i}\]と表されるので、
平均個体数$\lambda_{i}$を対数リンク関数と線形予測子を使って以下の式で表される。
\[\begin{align} \lambda_{i} &=A_{i}\exp(\beta_{1}+\beta_{2}x_{i}) \\ &=\exp (\beta_{1}+\beta_{2}x_{i}+\log A_{i}) \end{align}\]このように面積をオフセット項として扱うことで、 人口密度のような割算値を直接目的変数とすることなくモデリングすることが可能となる。
観測データの概要
%matplotlib inline
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.font_manager as fm
data = pd.read_csv('~/Downloads/data4b.csv')
fp = fm.FontProperties(fname='/Library/Fonts/Yu Gothic Medium.otf', size=12)
data.info()
print()
print(data.describe())
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 100 entries, 0 to 99
Data columns (total 3 columns):
y 100 non-null int64
x 100 non-null float64
A 100 non-null float64
dtypes: float64(2), int64(1)
memory usage: 2.4 KB
y x A
count 100.000000 100.000000 100.000000
mean 48.090000 0.514100 10.468000
std 17.137056 0.188573 2.927262
min 13.000000 0.050000 3.500000
25% 36.000000 0.400000 8.800000
50% 46.000000 0.515000 10.300000
75% 59.500000 0.642500 12.150000
max 95.000000 0.990000 17.400000
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.scatter(data.A[data.x < 0.2], data.y[data.x < 0.2], label='0.0-0.2', c='w')
ax.scatter(data.A[(data.x >= 0.2) & (data.x < 0.4)],
data.y[(data.x >= 0.2) & (data.x < 0.4)], label='0.2-0.4', c='y')
ax.scatter(data.A[(data.x >= 0.4) & (data.x < 0.6)],
data.y[(data.x >= 0.4) & (data.x < 0.6)], label='0.4-0.6', c='b')
ax.scatter(data.A[(data.x >= 0.6) & (data.x < 0.8)],
data.y[(data.x >= 0.6) & (data.x < 0.8)], label='0.6-0.8', c='g')
ax.scatter(data.A[(data.x >= 0.8) & (data.x < 1.0)],
data.y[(data.x >= 0.8) & (data.x < 1.0)], label='0.8-1.0', c='r')
ax.legend(loc='upper left')
ax.set_xlabel('調査地の面積 A', fontproperties=fp)
ax.set_ylabel('植物の個体数 y', fontproperties=fp)
ax.set_title('散布図', fontproperties=fp)
fig.show()
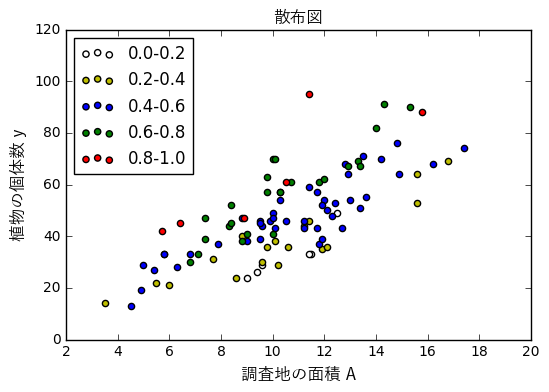
オフセット項つきポワソン回帰でfitting
import statsmodels.api as sm
import statsmodels.formula.api as smf
glm = smf.glm(formula='y ~ x', data=data, offset=np.log(data.A),
family=sm.families.Poisson())
res = glm.fit()
print(res.summary())
Generalized Linear Model Regression Results
==============================================================================
Dep. Variable: y No. Observations: 100
Model: GLM Df Residuals: 98
Model Family: Poisson Df Model: 1
Link Function: log Scale: 1.0
Method: IRLS Log-Likelihood: -323.17
Date: Tue, 13 Dec 2016 Deviance: 81.608
Time: 07:10:13 Pearson chi2: 81.5
No. Iterations: 7
==============================================================================
coef std err z P>|z| [95.0% Conf. Int.]
------------------------------------------------------------------------------
Intercept 0.9731 0.045 21.600 0.000 0.885 1.061
x 1.0383 0.078 13.364 0.000 0.886 1.191
==============================================================================
def gen_ytest(res, x: float, Arange: np.array):
xrange = [x for i in range(0, len(Arange))]
x_test = pd.DataFrame({'x': xrange, 'A': Arange})
return res.predict(x_test, offset=np.log(x_test.A))
Arange = np.arange(0, 18, 0.1)
ytest_01 = gen_ytest(res, 0.1, Arange)
ytest_03 = gen_ytest(res, 0.3, Arange)
ytest_05 = gen_ytest(res, 0.5, Arange)
ytest_07 = gen_ytest(res, 0.7, Arange)
ytest_09 = gen_ytest(res, 0.9, Arange)
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.scatter(data.A[data.x < 0.2], data.y[data.x < 0.2], label='0.0-0.2', c='black')
ax.plot(Arange, ytest_01, c='black', label='x=0.1')
ax.scatter(data.A[(data.x >= 0.2) & (data.x < 0.4)],
data.y[(data.x >= 0.2) & (data.x < 0.4)], label='0.2-0.4', c='b')
ax.plot(Arange, ytest_03, c='b', label='x=0.3')
ax.scatter(data.A[(data.x >= 0.4) & (data.x < 0.6)],
data.y[(data.x >= 0.4) & (data.x < 0.6)], label='0.4-0.6', c='y')
ax.plot(Arange, ytest_05, c='y', label='x=0.5')
ax.scatter(data.A[(data.x >= 0.6) & (data.x < 0.8)],
data.y[(data.x >= 0.6) & (data.x < 0.8)], label='0.6-0.8', c='g')
ax.plot(Arange, ytest_07, c='g', label='x=0.7')
ax.scatter(data.A[(data.x >= 0.8) & (data.x < 1.0)],
data.y[(data.x >= 0.8) & (data.x < 1.0)], label='0.8-1.0', c='r')
ax.plot(Arange, ytest_09, c='r', label='x=0.9')
ax.set_xlabel('植物の体サイズ x', fontproperties=fp)
ax.set_ylabel('生存種子数 y', fontproperties=fp)
ax.legend(loc='best', fontsize=10, prop=fp)
ax.set_title('散布図', fontproperties=fp)
fig.show()
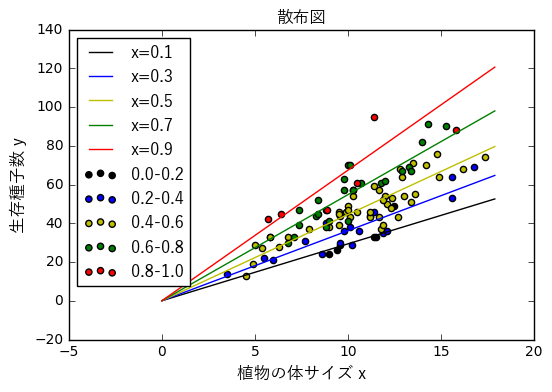
まとめ
- 観測値どうしの割算値作成はせず、ロジスティック回帰やオフセット項つき回帰などを用いる