はじめてのパターン認識 第11章 bagging

はじめてのパターン認識 第11章のbaggingについてまとめた。
baggingとは
学習データのブートストラップサンプルを用いて複数の弱学習器を独立に学習させ、
それらを組み合わせて強学習器を作るアンサンブル学習の1種。
分類問題では多数決で、回帰問題では平均をとることで
新しい入力サンプルに対する予測をおこなう。
ちなみにブートストラップサンプリングとは、
サンプル集合$X$から重複ありで抽出して新たなサンプル集合$X^{‘}$を作る手法である。
特徴
- 各学習器は独立しているため
学習を並列化して学習時間を短縮させることができる。 - バリアンスを低減できるため
弱学習器には高バリアンスな決定木などがよく使用される。 - 多数決or平均をとるため過学習を防ぐことができる。
そのため、最大までノードを分割した木が使うのが良い。 - 学習器が持つばらつきにはブートストラップサンプルのばらつきが反映されるのみなので、
決定木の相関が高くなってしまい十分な性能強化ができない可能性がある。
- この点を改良したのがboostingやrandom forestである。
アルゴリズム
- 学習データ: $\mathbf{x}_{i}\in \mathbb{R}^{d}, t_{i}=\{-1, +1\}\quad(i=1,\cdots,N)$
- 弱学習器: $y_m(\mathbf{x})\quad(m=1,\cdots,M)$
- 識別問題: $y_m(\mathbf{x})=\{-1,+1\}$
- 回帰問題: $y_m(\mathbf{x})\in\mathbb{R}$
- 各学習器$y_{m}$において、ブートストラップサンプルを用いて独立に学習
- 入力$\mathbf{x}$に対する予測値$Y_{M}$を出力する。
- 識別問題の場合: $y_{M}$の多数決
- 回帰問題の場合: $Y_{M}(\mathbf{x})=\frac{1}{M}\sum_{i=1}^{M}y_{m}$
実践
sklearn.ensemble.BaggingClassifierでirisデータセットを分類する。
%matplotlib inline
import os
import sys
sys.path.append(os.path.abspath('{}/../../'.format(os.getcwd())))
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.cross_validation import KFold
from sklearn.ensemble import BaggingClassifier
from sklearn.metrics import accuracy_score
num_iterations = 100
iris = load_iris()
y_pred_tr_list = []
y_pred_te_list = []
for n_est in range(num_iterations):
n_est += 1
tr_list = []
te_list = []
kf = KFold(len(iris.data), n_folds=5)
for tr_idx, te_idx in kf:
x_tr, x_te = iris.data[tr_idx], iris.data[te_idx]
y_tr, y_te = iris.target[tr_idx], iris.target[te_idx]
clf = BaggingClassifier(n_estimators=n_est)
clf.fit(x_tr, y_tr)
y_tr_pred = clf.predict(x_tr)
y_te_pred = clf.predict(x_te)
#print('oob_score: {}'.format(round(clf.oob_score, 5)))
tr_list.append(accuracy_score(y_tr, y_tr_pred))
te_list.append(accuracy_score(y_te, y_te_pred))
y_pred_tr_list.append(sum(tr_list)/len(tr_list))
y_pred_te_list.append(sum(te_list)/len(te_list))
y_pred_tr_sr = pd.Series(y_pred_tr_list)
y_pred_tr_sr.plot(grid=True, color='b', ylim=(None, 1.005))
plt.xlabel('num estimators')
plt.ylabel('accuracy')
plt.title('accuracy against training data')
plt.show()
y_pred_te_sr = pd.Series(y_pred_te_list)
y_pred_te_sr.plot(grid=True, color='b')
plt.xlabel('num estimators')
plt.ylabel('accuracy')
plt.title('accuracy against test data')
plt.show()
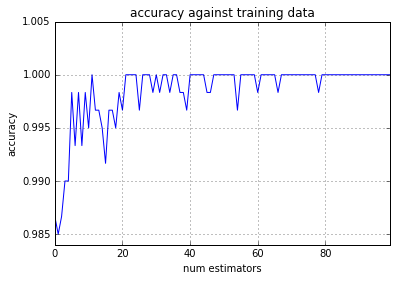
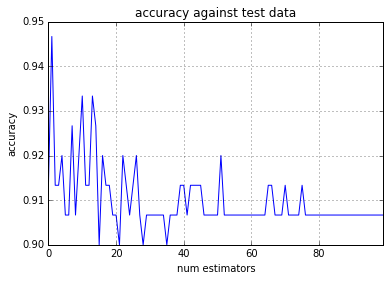
弱学習器の数を増やしても過学習を起こしていないことがわかる。
from IPython.display import Image
import swsk
graph = swsk.tree.get_tree_graph(clf.estimators_[0], iris)
Image(graph.create_png())
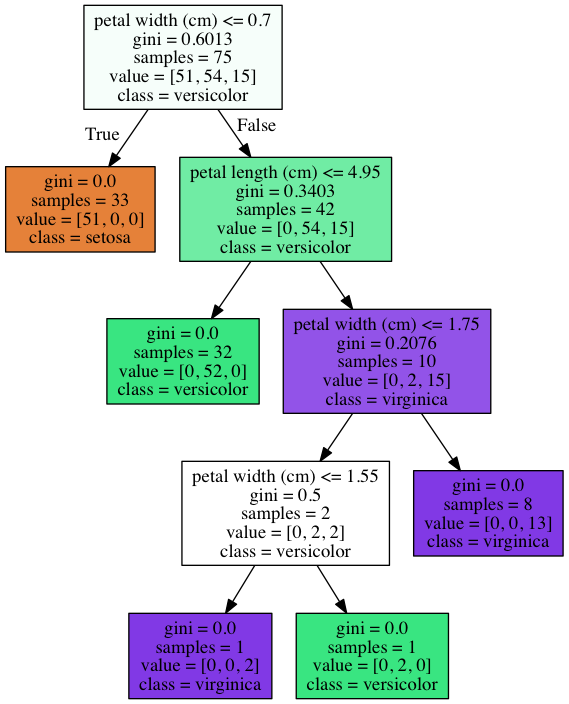
このようにノード数の多いややover-fitting気味な木でも
baggingにより複数の弱学習器を組み合わせることで過学習を防ぐことができている。