はじめてのパターン認識 第11章 決定木

はじめてのパターン認識 第11章の決定木についてまとめた。
決定木とは
決定木とは、if ... then ... elseのような単純な識別規則を組み合わせて
分類・回帰をおこなうノンパラメトリックな手法である。
以下の説明はCARTを前提とする。
特徴
- 学習した木を可視化することができる。
- 質的変数も量的変数も扱うことができる。
- ノード数を増やすと過学習しやすいのでノード数の調整が必須。
- 訓練データにfitしやすく、高バリアンスである。
木の分割
- $C_{i}\quad(i=1,\cdots,K)$: クラス
- $N(t)\quad(t=1,\cdots,T)$: ノード$t$に属するサンプルの数
- $N_{j}$: クラス$j$に属するサンプルの数
- $N_{j}(t)$: ノード$t$に属するサンプルのうちクラス$j$に属する数
- $p(t)=\frac{N(t)}{N}$: サンプルがノード$t$に属する確率
- $P(C_{j})=\frac{N_{j}}{N}$: クラス$j$の事前確率
- $p(t|C_{j})=\frac{N_{j}(t)}{N_{j}}$: クラス$j$のサンプルがノード$t$に属する確率
ノード$t$におけるクラス$j$の事後確率$P(C_{j}|t)$は、ベイズの公式より
\[\begin{align} P(C_{j}|t) &=\cfrac{p(t|C_{j})P(C_{j})}{p(t)} \\ &=p(t|C_{j})P(C_{j})p(t)^{-1} \\ &=\cfrac{N_{j}(t)}{N_{j}} \cfrac{N_{j}}{N} \cfrac{N}{N(t)} \\ &=\cfrac{N_j(t)}{N(t)} \end{align}\]となる。
不純度(impurity)
ノード$t$で分割規則を作るときは不純度の減り方が最も大きな分割を選ぶ。
- $t_{L}$: 子ノード(左)
- $t_{R}$: 子ノード(右)
- $p_{L}$: サンプル$\mathbf{x}$が$t_{L}$に属する確率
- $p_{R}$: サンプル$\mathbf{x}$が$t_{R}$に属する確率
とすると、
\[\Delta I(s,t)=I(t)-\left(p_{L}I(t_{L})+p_{R}I(t_{R}) \right)\]ノード$t$の不純度$I(t)$を
\[I(t)=\phi\left( P(C_{1}|t), \cdots,P(C_{K}|t) \right)\]と定義すると、$\phi()$は、
- $P(C_{i}|t)=\frac{1}{K}\quad(i=1,\cdots,K)$のとき、
すなわちどのクラスの事後確率も一様に等しいとき最大になる。 - ある$i$について$P(C_{i}|t)=1$となり、$j \neq i$のときは$P(C_{j}|t)=0$、
すなわちただ1つのクラスに定まるとき最小になる。 - $P(C_{i}|t)\quad(i=1,\cdots,K)$に関して対称な関数である。
という性質をもつ。
誤り率
\[I(t)=1-\max_{i}P(C_{i}|t)\]ノード$t$において事後確率$P(C_{j}|t)$が最大となるクラスを選ぶ。
交差エントロピー
\[I(t)=-\sum_{i=1}^{K} P(C_{i}|t) \ln P(C_{i}|t)\]ジニ係数
\[\begin{align} I(t) &=\sum_{i=1}^{K} \sum_{j \neq i} P(C_{i}|t)P(C_{j}|t) \\ &=\sum_{i=1}^{K} P(C_{i}|t)\left( 1-P(C_{i}|t) \right) \\ &=1-\sum_{i=1}^{K} P(C_i|t)^2 \end{align}\]ジニ係数とは、 あるノードから取り出したサンプルを取り出し
そのサンプルが$i$番目のクラスであるときを1、
それ以外のクラスであるときを0とするベルヌーイ試行を考えたとき、
取り出したサンプルのクラスが異なる確率である。
取り出したサンプルのクラスが異なる確率が大きい
$=$そのノードに属するサンプルのクラスの偏りが小さい
(1のクラスと0のクラスがほぼ同程度存在する)
$=$不純度が大きい
ということを示している。
また、$P(C_{i}|t)\left( 1-P(C_{i}|t) \right)$はこのベルヌーイ試行の分散なので、
ジニ係数はすべてのクラスに関する分散の和でもある。
なお、ジニ係数はもともとは経済学において
所得分配の不均衡の度合いを示す指標である。
木の剪定 (pruning)
木が大きくなるとバイアスは小さくなるものの汎化性能が下がる、
木が小さいとバイアスが大きくなり再代入誤り率が大きくなる
というトレードオフの調整のために、
誤り率と木の複雑さで決まる許容範囲まで木を剪定する。
- $t\in \tilde{T}$: 終端ノード
- $M(t)$: 終端ノードに属するサンプルのうち、事後確率を最大にしないクラスのサンプル数
- $\alpha$: 1つの終端ノードがあることによる複雑さのコスト
とすると、木全体の誤り率と複雑さのコスト$R_{\alpha}(T)$は
\[\begin{align} R_{\alpha}(T) &= \sum_{t\in \tilde{T}} R(t) + \alpha |\tilde{T}| \\ &= \sum_{t\in \tilde{T}} \cfrac{M(t)}{N} + \alpha |\tilde{T}| \end{align}\]目的は木のコスト$R_{\alpha}(T)$を最小にすることであるが、
$\alpha$は誤り率と複雑さのバランスをとる正則化パラメータの役割を果たす。
続きは後日追記予定。
ちなみにscikit-learnでは木のpruningはサポートされていない。
そのため、max_depthやmax_leaf_nodeの値を
汎化性能を見ながら調整する必要がある。
実践
irisデータセットをsklearn.tree.DecisionTreeClassifierで分類、
bostonデータセットをsklearn.tree.DecisionTreeClassifierで回帰させる。
分類木
import os
import sys
sys.path.append(os.path.abspath('{}/../../'.format(os.getcwd())))
from sklearn.datasets import load_iris
from sklearn.cross_validation import train_test_split
from sklearn.metrics import accuracy_score
from IPython.display import Image
import swsk
# http://pythondatascience.plavox.info/scikit-learn/scikit-learn%E3%81%A7%E6%B1%BA%E5%AE%9A%E6%9C%A8%E5%88%86%E6%9E%90/
# http://sucrose.hatenablog.com/entry/2013/05/25/133021
# load dataset
iris = load_iris()
print(iris.target_names)
print(iris.feature_names)
# split dataset into training and test subsets
tr_x, te_x, tr_y, te_y = train_test_split(iris.data, iris.target, test_size=0.4)
print(tr_x.shape, tr_y.shape)
print(te_x.shape, te_y.shape)
# learn
clf = swsk.tree.DTClassifier(tr_x, tr_y, {'max_depth': 3})
# accuracy
pred_tr_y = clf.predict(tr_x)
pred_te_y = clf.predict(te_x)
print('accuracy against tr data: {}'.format(round(accuracy_score(tr_y, pred_tr_y), 5)))
print('accuracy against te data: {}'.format(round(accuracy_score(te_y, pred_te_y), 5)))
# show tree
graph = clf.graph(iris)
Image(graph.create_png())
['setosa' 'versicolor' 'virginica']
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
(90, 4) (90,)
(60, 4) (60,)
accuracy against tr data: 0.98889
accuracy against te data: 0.96667
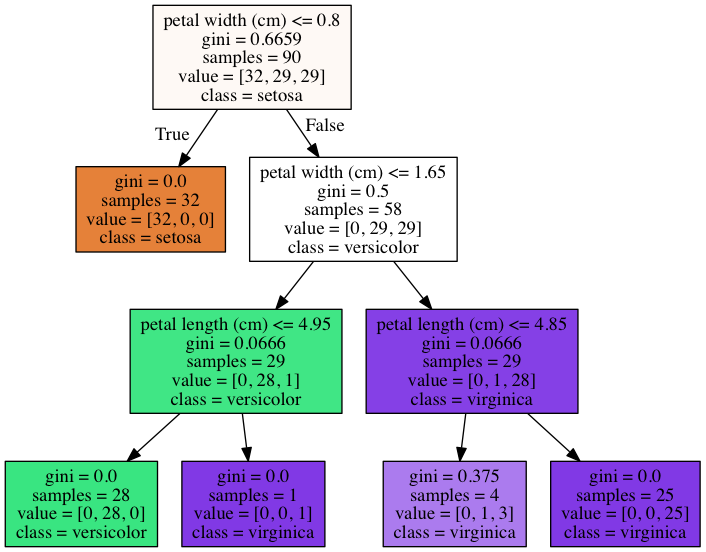
ジニ係数が小さくなるようにノードを分割している。
なお、criterion='entropy'とすれば不純度を交差エントロピーに変更できる。
回帰木
import os
import sys
sys.path.append(os.path.abspath('{}/../../'.format(os.getcwd())))
from sklearn.datasets import load_boston
from sklearn.cross_validation import train_test_split
from sklearn.metrics import mean_squared_error
from IPython.display import Image
import swsk
# load dataset
boston = load_boston()
print(boston.feature_names)
# split dataset into training and test subsets
tr_x, te_x, tr_y, te_y = train_test_split(boston.data, boston.target, test_size=0.4)
print(tr_x.shape, tr_y.shape)
print(te_x.shape, te_y.shape)
# learn
clf = swsk.tree.DTRegressor(tr_x, tr_y, {'max_depth': 3})
# accuracy
pred_tr_y = clf.predict(tr_x)
pred_te_y = clf.predict(te_x)
print('mse against tr data: {}'.format(round(mean_squared_error(tr_y, pred_tr_y), 5)))
print('mse accuracy against te data: {}'.format(round(mean_squared_error(te_y, pred_te_y), 5)))
# show tree
graph = clf.graph(boston)
Image(graph.create_png())
['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO'
'B' 'LSTAT']
(303, 13) (303,)
(203, 13) (203,)
mse against tr data: 11.95696
mse accuracy against te data: 30.75719
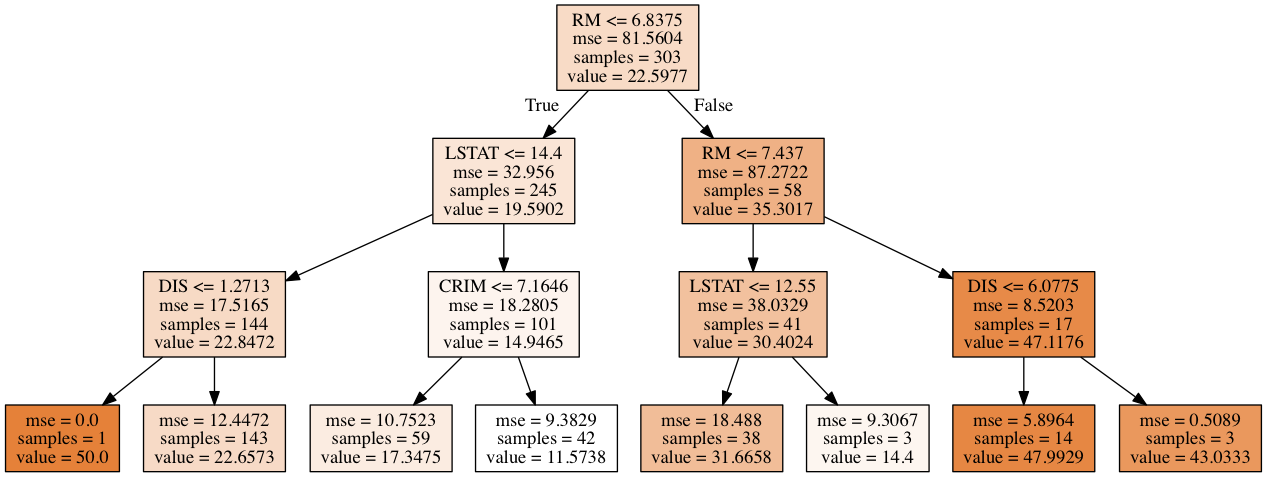
回帰木では、不純度にmean squared errorが使用されている。
章末問題
11.1
決定木Aの$(C_{1}, C_{2})=(50,150)$のノードを$t_{A,L}$, $(150,50)$のノードを$t_{A,R}$、
決定木Bの$(C_{1}, C_{2})=(100,200)$のノードを$t_{B,L}$, $(100,0)$のノードを$t_{B,R}$とする。
- $P(C_{1}|t_{A,L})=\frac{50}{200}=\frac{1}{4},\quad P(C_{2}|t_{A,L})=\frac{150}{200}=\frac{3}{4}$
-
$P(C_{1}|t_{A,R})=\frac{150}{200}=\frac{3}{4},\quad P(C_{2}|t_{A,R})=\frac{50}{200}=\frac{1}{4}$
- $P(C_{1}|t_{B,L})=\frac{100}{300}=\frac{1}{3},\quad P(C_{2}|t_{B,L})=\frac{200}{300}=\frac{2}{3}$
- $P(C_{1}|t_{B,R})=\frac{100}{100}=1,\quad P(C_{2}|t_{B,R})=\frac{0}{100}=0$
(1)
決定木Aの誤り率は$\frac{50}{400}+\frac{50}{400}=\frac{1}{4}$
決定木Bの誤り率は$\frac{100}{400}+\frac{0}{400}=\frac{1}{4}$
よって、どちらの木も誤り率は同じである。
(2)
決定木Aの総コスト$R_{A}(T)$は
\[\begin{align} R_{A}(T) &= \sum_{t\in \{t_{A,L}, t_{A,R}\}} R(t) + \alpha |\tilde{T}| \\ &= -\sum_{t\in \{t_{A,L}, t_{A,R}\}} \sum_{i=1}^{2} P(C_{i}|t) \ln P(C_{i}|t) + \alpha |\tilde{T}| \\ &= -2 \left( \frac{1}{4}\ln\frac{1}{4} + \frac{3}{4}\ln\frac{3}{4} \right) + 2\alpha\\ &= 0.562335\cdots \times 2 + 2\alpha \\ &= 1.125 + 2\alpha \end{align}\]決定木Bの総コスト$R_{B}(T)$は
\[\begin{align} R_{B}(T) &= \sum_{t\in \{t_{B,L}, t_{B,R}\}} R(t) + \alpha |\tilde{T}| \\ &= -\sum_{t\in \{t_{B,L}, t_{B,R}\}} \sum_{i=1}^{2} P(C_{i}|t) \ln P(C_{i}|t) + \alpha |\tilde{T}| \\ &= - \left(\frac{1}{3}\ln\frac{1}{3} + \frac{2}{3}\ln\frac{2}{3} + \ln1 \right) + 2\alpha \\ &= 0.6365\cdots + 2\alpha \end{align}\]よって、決定木Bの方が総コストが低い。
(3)
決定木Aの総コスト$R_{A}(T)$は
\[\begin{align} R_{A}(T) &= \sum_{t\in \{t_{A,L}, t_{A,R}\}} R(t) + \alpha |\tilde{T}| \\ &= \sum_{t\in \{t_{A,L}, t_{A,R}\}} \sum_{i=1}^{2} P(C_{i}|t) (1 - P(C_{i}|t)) + \alpha |\tilde{T}| \\ &= 2 \left( \frac{1}{4}\times\frac{3}{4} + \frac{3}{4}\times\frac{1}{4} \right) + 2\alpha\\ &= \frac{3}{4} + 2\alpha \end{align}\]決定木Bの総コスト$R_{B}(T)$は
\[\begin{align} R_{B}(T) &= \sum_{t\in \{t_{B,L}, t_{B,R}\}} R(t) + \alpha |\tilde{T}| \\ &= \sum_{t\in \{t_{B,L}, t_{B,R}\}} \sum_{i=1}^{2} P(C_{i}|t) (1 - P(C_{i}|t)) + \alpha |\tilde{T}| \\ &= 2 \left( \frac{1}{3}\times\frac{2}{3} + 1\times0 \right) + 2\alpha\\ &= \frac{4}{9} + 2\alpha \end{align}\]よって、決定木Bの方が総コストが低い。